Simultaneous Equations
- Maths Pi-rates
- Nov 8, 2017
- 3 min read
In exams, simultaneous equations usually come up with two equations, two unknowns, and the need to find the value of both unknowns. These unknowns can be anything varying between a to z, but the most common situation that will come up is the need to find the value of x and y. Please note that the appearance of the unknown (so whether or not it is a, b, c, or any other letter possible) doesn't affect the answer, nor should it affect how you work it out.
Here's an example to explain how to solve simultaneous equations.
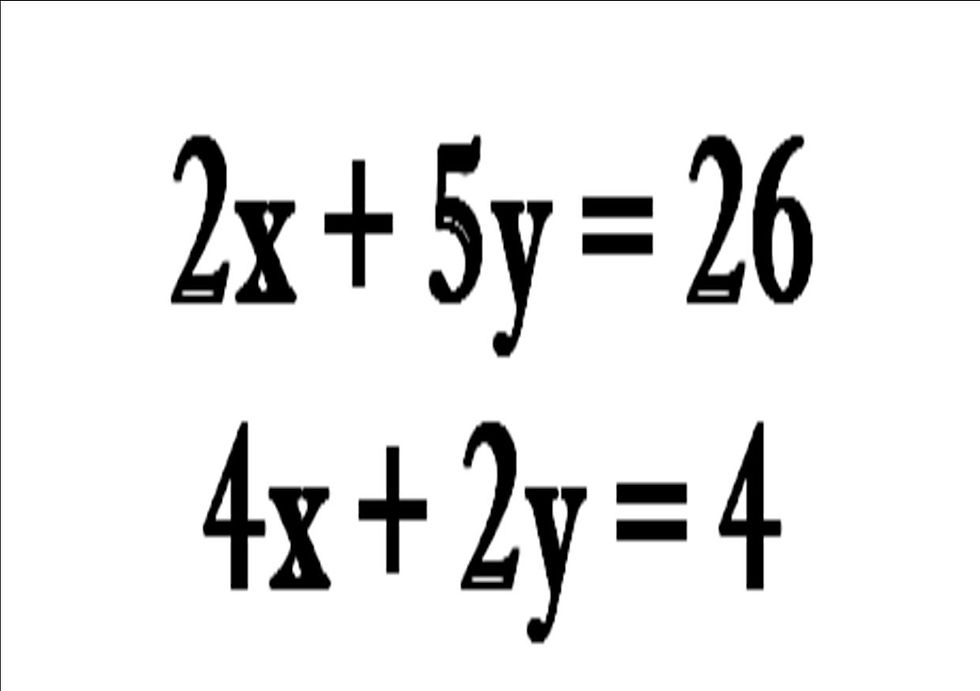
Example 1
In this example, the first unknown here is x and the second unknown which is y. At the moment, the value of both of these letters are unknown and it would be impossible to work the value out using only one equation. In both equations there is no common coefficient.
Coefficient - A coefficient is a numerical constant placed before, and multiplying, an algebraic expression.
So in this example, 4, 5 and 2 are all coefficients; 4 is the coefficient of the algebraic expression x, and the coefficient of y is 5.
The first step to solving simultaneous equations is to make a set of common coefficients; you can make either both the coefficients of y the same (so making 5y and 2y the same in value) or the coefficients of x the same (so making 2x and 4x the same in value). You can do this by multiplying the two equations. It is advisable to mark the equations one and two. Choosing to make the y coefficients the same, I multiply 2x+5y=26 by 2 and 4x+2y=4 by 5 to give me:
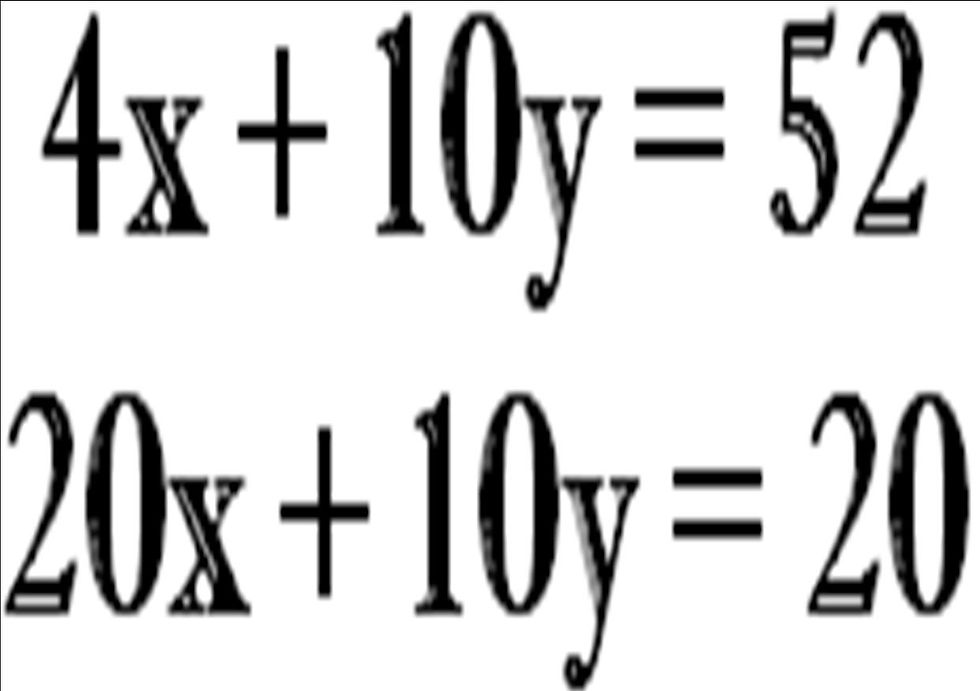
As you can see here, we now have a common coefficient of y which is 10; so 10 multiplied by the constant y will give the same answer in both equations because y is the same value in both equations. For example, say y was 5, 10(5)=50. Both my y coefficients are the same.
Now that both coefficients are the same, we can cancel those coefficients out of the equation to leave us with only one unknown. To do this we need to look at the function sign before the common coefficient. In this example we have two + symbols. This means we need to subtract the entire lower equation from the top equation. The reason as to why we do this is because, to cancel out 10y from the equation when we add or subtract the equations. To work out if I needed to add or subtract I would look at the first coefficient which is + 10y and think what I needed to do so that I got 0. Answer: I'd subtract 10y.
Because I need to subtract 10y I'd subtract the entire lower equation away from the top equation so that I got:
-16x = 32
Notice how now I have one equation and only one unknown which is x. From hereon it is basic algebra where I make x the subject. To do this I would divide -16 from both sides (as whatever you do to one side you must do to the other) which would leave me with:
x = -2
Now we have the value of the unknown x, but we still need to find the value of y and to do this we simply substitute x back into the original equation.
2(-2) + 5y = 26
-4 +5y = 26
5y = 30
y = 6
After substituting the x value into the original equation and rearranging so that y is the subject of the equation, we work out that x = -2 and y = 6.
Let's Recap...
Here's a quick summary of how to solve simultaneous equations:
Firstly, you make a common coefficient
Cancel out the coefficient from the equation by adding or subtracting the lower equation from the top equation so that it leaves only one unknown and one equation.
Rearrange and solve what's left of this new equation to find the first value
Substitute first value into the original equation and then rearrange to find the second value.
Questions
Here's a few questions for you to try:
1) 4x + 3y = 17
2x + 4y = 16
2) 2x + 3y = 20
5x - y = 16
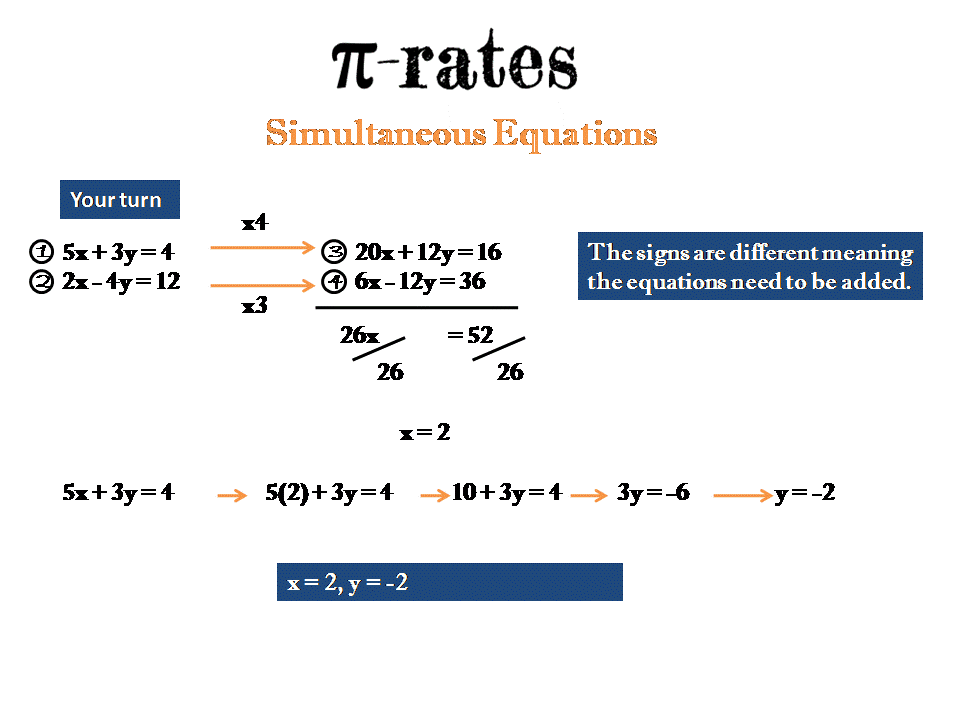
3) 5x + 3y = 4
2x - 4y = 12
Answers and Solutions
1)

2)
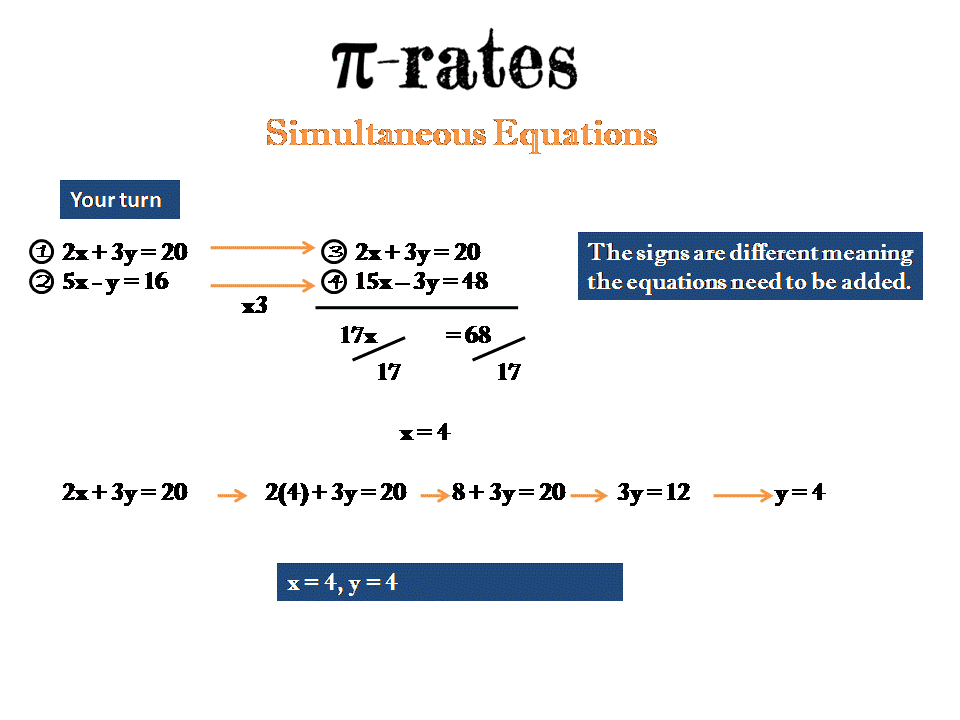
3)











Comments